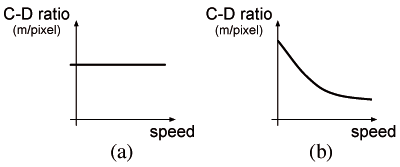
(a) constant C-D ratio (b) mouse acceleration
We introduce semantic pointing, a novel interaction technique that improves target acquisition in graphical user interfaces (GUIs). Semantic pointing uses two independent sizes for each potential target presented to the user: one size in motor space adapted to its importance for the manipulation, and one size in visual space adapted to the amount of information it conveys. This decoupling between visual and motor size is achieved by changing the control-to-display ratio according to cursor distance to nearby targets. We present a controlled experiment supporting our hypothesis that the performance of semantic pointing is given by Fitts' index of difficulty in motor rather than visual space. We apply semantic pointing to the redesign of traditional GUI widgets by taking advantage of the independent manipulation of motor and visual widget sizes.
Categories and Subject Descriptors: H.5.2 [Information Interfaces and Presentation (e.g., HCI)]: User Interfaces — Graphical user interfaces, Input devices and strategies, Interaction styles, Theory and methods
Keywords : Control-display ratio, Fitts' law, graphical user interface, pointing, semantic pointing.
Copyright ACM, (2004).
This is the author's version of the work.
It is posted here by permission of ACM for your personnal use.
Not for redistribution.
The definitive version was published in Proceedings of the 2004 conference
on Human factors in computing systems (CHI 2004).
[http://doi.acm.org/10.1145/985692.985758]
Pointing is a fundamental task in graphical user interfaces (GUIs). To help manage the growing complexity of software, such as the increasing number of toolbars and menu commands, the HCI literature has introduced new interaction techniques that attempt to reduce pointing time. This paper explores the idea of assigning two separate sizes for objects in the interface: a visual size for display, and a motor size reflecting the importance of the object for interaction. We hypothesize that task difficulty depends on the motor, not visual size of objects, and control the motor size by adapting the control-display (C-D) ratio. We call this technique semantic pointing, since motor sizes are used to reflect the local semantics of the screen.
Fitts' law [6] is widely used to design and evaluate interaction techniques and input devices [16]. It links the movement time (MT) to acquire a target to the task's index of difficulty (ID). ID is the logarithm of the ratio between target distance (D) and target width (W). MT is a linear function of ID characterizing the system. The implications of Fitts' law have been used in several techniques to facilitate pointing tasks by enlarging the target or by reducing its distance [4, 1, 18, 5, 24].

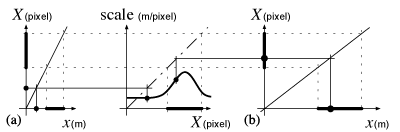
Control-display ratio adaptation [13, 23, 5] is another approach for facilitating target acquisition. This technique improves pointing performance but has not been analyzed in terms of Fitts' law, and its possible use in real GUIs has not been fully explored. The C-D ratio [17] is a coefficient that maps the physical displacement of the pointing device to the resulting on-screen cursor movement in a system where there is an indirection between the pointing device and the display (typically with a mouse). The C-D ratio defines the distance the mouse has to cover in the physical world (dx in meter) to move the cursor on the screen by a given distance (dX in pixel)1. 1We use the following conventions: capital letters denote quantities (e.g. distances) concerning the screen, while lower case letters denote those concerning the physical world. For distances, we use two different units (pixel and meter respectively) to disambiguate ratios that would otherwise be dimensionless. The C-D ratio is dx/dX. A typical C-D ratio adaptation is the so-called mouse “acceleration”. The cursor moves by a larger distance when the mouse covers a given amplitude more quickly (Figure 1), capturing an intention: when users move the physical device quickly, they typically wish to go further, so the cursor can be displaced even faster to cover the distance more quickly.
After reviewing previous work on facilitating target acquisition, we describe semantic pointing and predict its effect on pointing performance in terms of Fitts' law. We then describe a controlled experiment that tests our predictions. Finally, we illustrate potential applications of semantic pointing to GUI design.
With respect to Fitts' law, there are two simple ways to reduce the difficulty of a pointing task: enlarging the target or moving it closer to the cursor. Both have been explored in several ways. A widely-used direct application of this principle is contextual pop-up menus. Such menus are displayed at the cursor location so that distances to the items are minimal. Pie menus [4] are even more radical: the distance from each menu item to the cursor is constant and very small. The distance can also be reduced by moving the potential targets of a directed movement towards the cursor, as in the drag-and-pop technique [1].
Another approach consists in modifying target size when the cursor is close enough. This can be achieved by magnifying the target [18], or by adding a “bubble” around it [5]. Evaluations and comparisons with other techniques [23, 5] show that target resizing facilitates pointing even if the expansion is late [18] and unpredictable [24]. The problem in applying such techniques to real GUIs is that in order to expand a target surrounded by other possible targets, its neighborhood must be shrunk and the magnified target then moves when the expansion focus changes [11]. As a consequence, no performance improvement can be observed for systems like the Mac OS X Dock [18, 24]. More generally, techniques that dynamically change the screen layout cause a spatial disorganization that limits their expected benefits (e.g., for menus, [21, 19]).
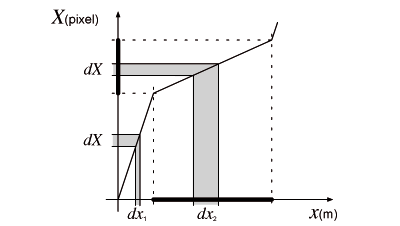
The C-D ratio is the ratio of the movement of the input device and the movement of the object it controls. The C-D ratio can be a constant (Figure 1a), a function of mouse speed as in mouse “acceleration” (Figure 1b), or a function of cursor position [23]. Increasing the C-D ratio when the cursor is within a target makes, at constant mouse speed, the cursor slow down: covering the same number of pixels requires moving the mouse by a longer displacement. Figure 2 illustrates this technique in one-dimensional (1D) space. The slope of the function mapping the screen to the physical world is the inverse of the C-D ratio. Within the target (shown as a thick black line), the C-D ratio is increased. Since the cursor stays longer within the target, it is easier for the user to acquire it.
Swaminathan and Sato [22] concluded that in the context of large displays “nonlinear mappings are too counterintuitive to be a general solution for pointer movement”. However such non-linear mappings have been successfully applied to 3D rotations [20] and 3D navigation [3], and most studies on pointing with C-D ratio adaptation [13, 23, 5] show a performance improvement. However, the effects of C-D ratio adaptation have always been interpreted in terms of feedback—“sticky” icons [23], pseudo-haptic feedback [14]—and have not been analyzed in terms of Fitts' law.
As explained below, C-D ratio adaptation can also be interpreted as a dynamic magnification of the physical motor space where the mouse movements take place. This relates to fisheye views and zoomable interfaces that use a local or global magnification of the visual space.
Fisheye views locally distort a visualization by magnifying a particular point—the focus—and contracting its neighborhood—the context—according to a degree of interest function based on a priori importance and distance to focus [7]. This technique has been applied to a variety of contexts and its impact on pointing has been studied [11]. As noted above, such techniques expand target sizes but the motion of the focus impairs target acquisition [18, 24]. Even fine-tuned versions of fisheye views do not compete with other techniques: hierarchical menus are better than fisheye menus [2], flat representations are better than distorted ones for focus targeting [11].
Igarashi and Hinckley's navigation technique [12] uses speed-dependent automatic zooming to enhance scrolling. It manipulates view magnification to keep a constant optical flow while scrolling at variable speed. Evaluations, however, failed to show a quantitative benefit on task completion time. This may be because the magnification level is controlled solely by the user—even if indirectly through the scrolling speed—and so does not automatically adapt to the task.
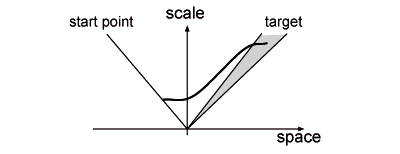
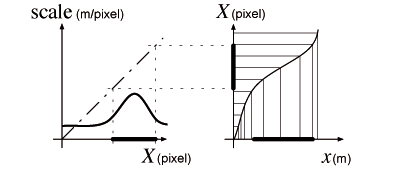
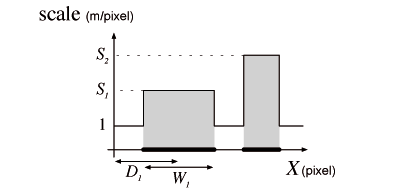
Furnas and Bederson introduced space-scale diagrams [8] to represent zoomable interfaces. Using a metric on trajectories—based on quantity of information—they predict optimal trajectories and observe that they match those empirically chosen by users, a fact confirmed by Guiard et al. [10]. Optimal trajectories have a scale adapted to the distance to the target: as the cursor approaches the target, the visual space is magnified, the cursor thus gains precision while slowing down in target space2 2The target space is not directly the screen space because magnification introduces a scaling factor. (Figure 3).
In summary, many researchers have used, explicitly or implicitly, the effects of C-D ratio adaptation to improve pointing performance, yet there is no unified approach for understanding these effects.
Semantic pointing relies on the following hypothesis: the difficulty of a pointing task is not directly linked to the on-screen representation of the task, but to the actual difficulty of the movement performed in the physical world to accomplish it. We first show that C-D ratio modification can be interpreted as a manipulation of the relative sizes of objects in visual and motor space. We then describe how semantic pointing affects pointing difficulty by making the C-D ratio a function of a context known to the system.
The C-D ratio defines the ratio between distances for the physical device and distances on the screen, or how the motor space is projected into the visual space. If the C-D ratio is a constant, then for a 1D world this projection is a linear function linking motor space (x in meters) to visual space (X in pixel) as illustrated in Figure 4. The slope of this function, in pixel/m, is the C-D gain and the inverse of this gain, in m/pixel, is the C-D ratio.
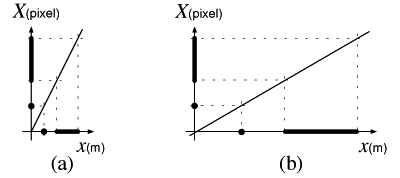
When the C-D ratio is low (Figure 4a) the motor space is contracted compared to a higher C-D ratio (Figure 4b). In fact, the C-D ratio can be seen as the motor space scale relative to the visual space (called simply ‘scale’ in the rest of the paper). At low scale, the movement to acquire a target is short but target size is also small. On the other hand, at high scale, the target distance is longer but the accuracy needed to acquire it is reduced. In any case the task difficulty remains the same since it is characterized by the non-dimensional ratio D/W which is insensitive to uniform scaling. In other words, uniform scaling does not affect the ID. This illustrates the trade-off between target distance and target size [17].
The principle of semantic pointing is to dynamically adapt the motor space scale to reduce both target distance and the accuracy needed to acquire it. The idea is to choose a low scale, adapted to the task extension D, when the cursor is far from any potential target (Figure 5a) and to choose a high scale, adapted to the task precision W, when the cursor is close enough to target (Figure 5b). Therefore, without changing the visual layout, the target may be nearer and bigger in motor space.
Instead of interpreting the contextual C-D ratio adaptation as the dynamic change of a linear function slope, we can interpret it as the local slope of a certain non-linear function. This is equivalent because the scale is only a function of position. As in a fisheye view, scale becomes a local property: some areas are expanded while others shrink. The scale function can be chosen so that the resulting distorted motor space has the following property: important areas for interaction, such as potential targets, are bigger while non-important areas, such as empty space, are shrunken (Figure 6). In empty space, accuracy is less necessary than speed, while near a target, accuracy becomes more important than speed. The distortion is then consistent with the goal of aiding target acquisition.
This “need for accuracy” is not uniform across the screen and depends, for each pixel, on whether it is part of a potential target, e.g. a button or icon, or part of empty space, e.g. a window background. As noticed by Guiard et al. [9], there is a mismatch between the abstract task of picking a target and a pointing task on screen. Selecting an icon on a typical desktop consists of pointing to a 48 × 48 pixel target on a 1600 × 1200 pixel screen, i.e. providing log2((1600 × 1200) / (48 × 48)) ≈ 10 bits of information to the system. For the user as well as for the system, however, the real information is only the choice of one icon within those present on the desktop. Choosing one icon among a set of 64 only requires log2(64) = 6 bits of information3. 3Those bits can be understood by thinking of a binary search: the target is (or not) in the first half of the set. This boolean is one bit of information and now the target is in a known set of 32 icons, etc.
By making scale dependent on pixel semantics, semantic pointing makes important pixels bigger in motor space, and thus helps to reduce the mismatch between the abstract selection task and its execution. By using information that is normally known to but ignored by the system, namely the potential targets, the amount of information the user needs to provide to the system can be reduced. The local “need for accuracy” is in fact a local information density expressing how relevant each pixel is to manipulation.
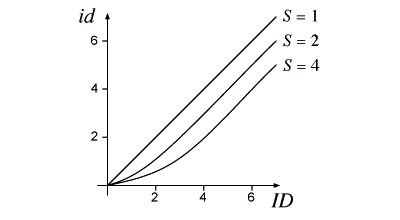
We have shown (see Appendix 1 for a detailed analysis) that computing the C-D ratio as a function of the distances from the cursor to potential targets, and of their importance, can change the effective tolerance on targets. For difficult tasks (when the target distance is much larger than target width), the task difficulty is then reduced by the number of bits of the motor scale. Figure 7 shows the relation between the usual difficulty (ID) and the one in motor space (id) for a motor scale of 1, 2 and 4. It shows that, for large IDs, the difficulty in motor space gains one bit each time the scale doubles.
We conducted a controlled experiment to evaluate the benefits of semantic pointing as predicted by our analysis.
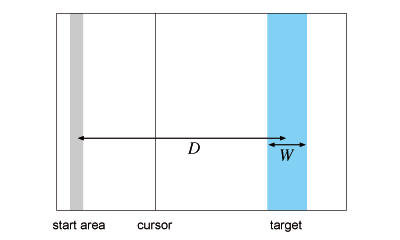
Participants had to perform successive 1D discrete pointing tasks. They had to move the cursor, represented by a one pixel thick vertical black line, to the start position marked by a gray rectangle on the left of the screen, rest there for 0.5 s, start moving to the target—a blue rectangle—as soon as it appeared on the right, and click it (Figure 8).
After each click, a visual signal indicated whether they have hit or not the target. After each block, their error rates were displayed and they were encouraged to conform to a nominal 4% error rate by speeding up or slowing down.
The first (control) condition held the scale constant, so the motor task was exactly the same as displayed. In the second (double) and third (quadruple) conditions, the scale was adapted accordingly to our model so that the target size was either doubled or quadrupled in motor space. We used the bell-shaped mixing function described in Appendix 1.
Five IDs (4, 5, 6, 7 and 8) and two sizes (D = 512 or 1024 pixel) were used, giving ten possible tasks. A series of 100 trials (10 times each possible task), consisting of every possible successive pair of tasks counter-balanced to account for order effects, was build. This series was repeated three times per participant, making each participant perform 300 trials.
Those series were split into 6 blocks consisting of 50 trials (5 times each task). An order for the three conditions was chosen for each participant. The first and fourth blocks were presented using the first condition, the second and fifth blocks using the second condition, and the third and last block using the third one. Each block was preceded by 10 randomly-chosen tasks using the same condition for practicing. This was chosen after a pilot study suggesting that, after ten trials, the movement times were stable.
Twelve unpaid adult volunteers, 11 male and one female, aged 27.2 years on average (SD = 6.10 years), served in the experiment. The six permutations of the three conditions order were repeated for pairs of subjects.
The pointing experiment was conducted on a 22-inch 1600 × 1200 resolution color monitor, using a Wacom Intuos 12×18 inch digitizing tablet with a puck. The baseline C-D ratio was set at the screen resolution (1cm on screen for 1cm in motor space) and the system had no mouse acceleration.
The effects of semantic pointing were explored by analyzing three dependent variables: reaction time (RT), movement time (MT), and error rate (ER). Repeated measures analyses of variance were performed on these three variables. We analyzed the effects of the three factors (3 conditions, 5 indices of difficulty, and 2 sizes) in a within-participant design.
No effect of the task size (D) on the three dependent variables was found to be statistically significant. This is consistent with Fitts' law and our model: both state that the performance of target acquisition is a function of the non-dimensional ratio D/W. The size effect is thus neglected for the rest of the analysis, and the following plots merge the two task sizes for each ID.
The reaction time (RT) was about 253 ms on average with small variations (SD = 75.76 ms). RT grew slightly with the task index of difficulty but this effect was not statistically significant. No significant difference was found among the three conditions.
The movement time (MT) as a function of the index of difficulty (ID) is plotted for the three conditions in Figure 9 (compare with the prediction in Figure 7). There was a significant effect of condition (F2,33 = 5.35, p = .0097) and ID (F4,55 = 30.04, p < .0001) on MT but no significant interaction between the two factors was found.
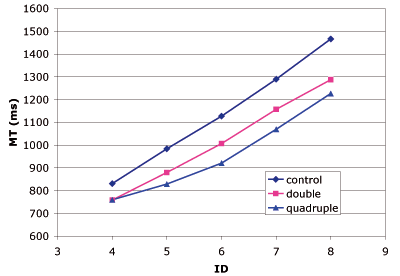
As predicted, the benefit of semantic pointing first grows with ID before remaining almost constant for difficult tasks. The maximum relative gain on task completion time is obtained for ID = 6 but for ID ≥ 5 the MT reduction is at least 10% (10.9% on average) for the double condition and at least 15% (16.9% on average) for the quadruple condition.
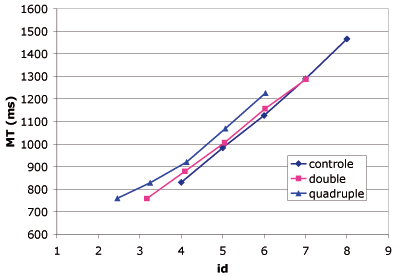
Figure 10 shows movement time as a function of index of difficulty in motor space (id). If our hypothesis that the performance of semantic pointing is given by Fitts' index of difficulty in motor rather than visual space is correct, the linear fit of MT should be better using id rather than ID as index of difficulty in Fitts' law. Table 1 gives the coefficient of simple determination (r2) and the root mean square error (RMSE) for both fits and shows that the difficulty in motor space better explains the variations of MT, thus validating our hypothesis.
| |||||||||||||
However, we can note on Figure 10 that for the
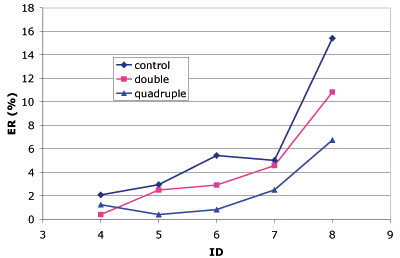
The participants were told to conform to a nominal 4% error rate (ER) on each block. The mean ER was in fact 4.26% but the differences between the three conditions are significant (Figure 11). On average, the ER was 6.2% in the control condition, 4.25% in the double one, and 2.35% in the quadruple one. The pointing movements were more accurate in the double and quadruple conditions than in the control condition for every ID, and, except for ID = 4, quadruple had a better ER than the other two conditions. So the reason why semantic pointing was not fully exploited to reduce target acquisition time is because it also served to enhance movement accuracy.
This argument is confirmed if we take a closer look at individual performances. The means reported in the foregoing are representative of most subjects, but there were individual strategies. Some participants took advantage of semantic pointing essentially by reducing their error rate; others conformed to the constant error rate requirement. Importantly, it is in the latter category of participants that performance was rigorously governed by the motor component of the task. This result confirms that semantic pointing unquestionably facilitates pointing, with this facilitation effect benefiting to various extents to target acquisition time and/or pointing accuracy. Furthermore, we conducted informal testing of a 2D desktop prototype4. 4A java applet simulating Semantic Pointing in 2D is available on line. We observed that users did not notice when semantic pointing was on or off and yet took advantage of it to improve their performance.
In this section we present applications of semantic pointing to GUI design.
In traditional GUIs, the size of an object is determined by visualization and manipulation constraints: the object must be big enough for the relevant information to be accessible to the user, and for the user to be able to manipulate it. When an object conveys little information, such as a button or scroll-bar, the size is determined by the manipulation constraint, wasting screen real-estate. Conversely, when a lot of information must be displayed, such as in a web page, the parts that can be manipulated, such as the links, may end up very small and difficult to interact with.
Semantic pointing resolves such conflicts by allowing two sizes to be set independently: the size in visual space, constrained by the information to be displayed, and the size in motor space, constrained by the importance of the object for manipulation. These sizes are manipulated through a new attribute, semantic importance (si), which amounts to the scale of motor-space size relative to visual-space size. When 0 < si < 1, the object is smaller in motor space than it appears in visual space, which is appropriate for objects whose manipulation is disabled, unlikely or dangerous; when si > 1, the object is bigger in motor-space than in visual space, making it easier to manipulate; si = 1 corresponds to traditional GUIs.
In order to redesign traditional GUI widgets such as scroll-bars, menus and buttons, we considered two aspects:
We show that semantic pointing can either reduce the screen footprint of widgets without affecting the interaction, or facilitate the interaction without affecting the screen layout.
The information provided by a traditional scroll-bar is rather poor: it specifies a position in the document and sometimes the proportion of the document that is currently displayed in the view. A typical scroll-bar uses a 15 pixel wide strip along the whole window (Figure 12a). However the same information can be conveyed by a much thinner strip, e.g. 3 pixel (Figure 12b). To make it possible for the user to manipulate the thumb and the arrow buttons, these are given a semantic importance of 5 so as to be as big in motor space as they were in the original design (Figure 12c5). 5The motor space distortion caused by semantic pointing is not accurately representable in euclidian geometry. Thus the representations in motor space cannot be exact and are given for illustration purposes.
The main real-estate constraint for menus is that labels must be readable, so the visual size of menu items cannot be reduced significantly (Figure 13a). However, the importance of menu items with respect to manipulation is variable. Disabled items and separators cannot be selected, so they can be given a small semantic importance, reducing the distance in motor space from the top of the menu to the items below them (Figure 13b).
As for menu items, the buttons and messages of a dialog box must be readable (Figure 14a). However, for the manipulation, only the buttons are relevant, so the rest of the box can be shrunken. Furthermore, the importance of the various buttons need not be equal. The default button, assumed to be the most likely choice, can be given a higher importance. More generally, the importance can be proportional to the probability of being selected (Figure 14b). “Dangerous” buttons can also be given a smaller importance to make them harder to select.

Similarly, the visual layout of rich documents such as web pages is often designed with aesthetics and visual communication in mind. But as far as interaction with such hyperdocuments is concerned, only the hyperlinks matter. Therefore, magnifying the hyperlinks in motor space should help users acquire them and improve navigation.
So far we have mostly considered semantic importance as a static attribute of interface objects. An exception is menu items, the importance of which vary according to their state: a disabled item has a low importance, which becomes high when the item is enabled. The same applies to disabled buttons in a dialog box. Another example where semantic importance can reflect the state of an object is the application icons in current desktops. When an application requires user attention, it blinks in the Microsoft Windows task-bar or its icon is animated in the Mac OS X Dock. Since the user is likely to click such an icon to activate the application, it would help to magnify it in motor space.
More elaborate strategies can be used to compute the semantic importance according to the state and history of the interaction. For example, applications in the Microsoft Office Suite have adaptive menus that reconfigure themselves so that the most often used items are at the beginning of the menu. The instability of menus is known to be a source of confusion for users [19, 21]. With semantic pointing, the importance of menu items can match the frequency of their use. This has a positive effect similar to adaptive menus, i.e. often-used commands are easier to reach, without disturbing the spatial layout of the menu items.
In this paper we introduced semantic pointing, a technique that disentangles motor space from visual space to facilitate pointing movements. We showed how to use C-D ratio adaptation to control the mapping between motor and visual space, interpreting it as a motor-space scale. We also showed that the index of difficulty of a pointing task is defined by the size of the target in motor rather than visual space. In addition, we observed that users did not notice the distortion introduced by semantic pointing, making the technique effective and yet transparent.
We presented several applications of semantic pointing to improve the design of traditional GUIs, by specifying the two sizes of each object with a new attribute: semantic importance. In some cases, the visual footprint of objects is reduced without changing their motor size, saving screen real-estate, while in other cases the visual layout is left untouched but the motor space is enlarged in order to facilitate interaction. We have also shown how the semantic importance of an object can change over time to adapt to the user's needs.
Our future work will concentrate on the problem of distractors. The presence of a potential target on the path of a pointing movement increases the distance to the real target, thus reducing the benefit of semantic pointing. We intend to study these effects systematically and experiment with techniques to minimize them. We also intend to explore more applications of semantic pointing and evaluate it in real settings.
The authors would like to thank the anonymous reviewers, the whole InSitu team, and especially Wendy Mackay, Caroline Appert and Stéphane Conversy, for their useful comments and suggestions about this work.
The simplest scale function that magnifies the pixels within a target is a step function (Figure 15). It can be defined using the rectangle function:
| Π(u) = 1 | for |u| ≤ 1/2 |
| 0 | otherwise |
For a target of size W at coordinate D the scale is then6: 6|X-D| is the euclidian distance from the cursor (X) to the target (D). The formulas are valid in any dimension.
scale(X) = (1 − Π(|X - D| / W)) + S × Π(|X - D| / W)
The first term of the sum takes the value 1 in empty space and 0 within the target whereas the second term takes the value S within the target and 0 outside. A generalized version for multiple targets is:
scale(X) = (1 - ∑iΠ(|X - Di| / Wi)) + ∑iSi × Π(|X - Di| / Wi),
where Dn, Wn and Sn are the position, size and scale of the nth target (Figure 15).
Since in a 1D world there is only one possible path linking two points, the target size in motor space can be computed by summing the scale function over the target:
| w = | ∫D - W/2D + W/2 scale(X) dX |
| = | S × W |
This size is the area of the grayed rectangles of Figure 15. If there is only one target7 7The influence of distractors will be studied in future work. we can similarly compute the target distance in motor space:
| d = | ∫0D scale(X) dX |
| = | (D - W/2) + S × W/2 |
The first term of this sum corresponds to the target distance in empty space and the second term to the supplemental distance added by the magnification of the target as the end of the movement runs across half of it. When D is small, the first term becomes negligible because the section of D that overlaps empty space tends toward zero. When D is much larger than W/2, it is the second term that becomes negligible. We can now predict the index of difficulty of the task8 8 We chose Fitts' formulation of the ID, rather than Shannon's [15], for the sake of convenience (analytical calculations are thus possible). It should be mentioned that this option has no effect on the bottom line of our argument. in motor space (id) as a function of the usual index of difficulty in visual space (ID) when the scale of the target is S:
Instead of using a simple rectangle function (Π), we use a bell-shaped function (Ω) as a mixing function to avoid discontinuities in the scale function. Figure 16 shows the differences between Π and Ω.
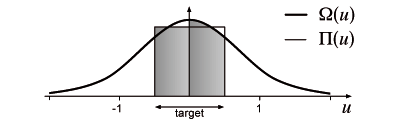
Like Π, Ω has been chosen to be compliant with the following fundamental requirements: correctly scaling the targets, i.e. ∫-1/21/2 Ω(u) du = 1, and rapidly decreasing towards zero when outside a target, i.e. ∫1/2∞ Ω(u) du ≤ 1 for example:
Ω(u) = ln(3) / cosh2(ln(3) × u)
This particular function was chosen because its integral can be computed analytically. The scale function then becomes:
scale(X) = (1 - ∑iΩ(|X - Di| / Wi)) + ∑iSi × Ω(|X - Di| / Wi),
and the relationship between id and ID has the same characteristics as with the rectangle version (Figure 7).